रीमैन की परिकल्पना, संख्या सिद्धांत में, जर्मन गणितज्ञ बर्नहार्ड रीमैन की परिकल्पना, रिमैन ज़ेटा फ़ंक्शन के समाधान के स्थान से संबंधित है, जो प्राइम नंबर प्रमेय से जुड़ा है और प्राइम संख्याओं के वितरण के लिए महत्वपूर्ण निहितार्थ हैं। रीमैन ने एक कागज में परिकल्पना को शामिल किया, "उबेर डाई अंजहल डेर प्रिमज़लेन अन्टर ईनर जेजेबेन ग्रोस" ("प्राइम नंबर की संख्या कम से कम एक मात्रा की तुलना में"), मोनाट्सबर्ते डेर बर्लिनर अकादेमी के नवंबर 1859 संस्करण में प्रकाशित हुआ ("मासिक समीक्षा" बर्लिन अकादमी के ")।
जीटा फ़ंक्शन को अनंत श्रृंखला के रूप में परिभाषित किया गया है s (s) = 1 + 2 −s + 3 + s + 4 mores + ⋯, या, अधिक कॉम्पैक्ट अंकन में, , जहां सकारात्मक पूर्णांक और s के माध्यम से 1 से अनंत तक n के लिए शब्दों का योग (of) 1 से अधिक एक निश्चित सकारात्मक पूर्णांक है। जेता फ़ंक्शन का पहली बार 18 वीं शताब्दी में स्विस गणितज्ञ लियोनहार्ड यूलर द्वारा अध्ययन किया गया था। (इस कारण से, इसे कभी-कभी यूलर ज़ेटा फ़ंक्शन कहा जाता है।) (1) के लिए, यह श्रृंखला केवल हार्मोनिक श्रंखला है, जिसे प्राचीन काल से बाउंड के बिना बढ़ाने के लिए जाना जाता है - यानी, इसका योग अनंत है।) यूलर ने तत्काल फेन हासिल किया 1735 में साबित कर दिया कि ζ (2) = π 2 /6, एक समस्या यह है कि युग के महानतम गणितज्ञों, स्विस Bernoulli परिवार (जेकब, जोहान, और डैनियल) सहित नहीं मिल पाया था। आम तौर पर, ईयूलर ने (1739) एक पूर्णांक और बर्नौली संख्या के लिए जेटा फ़ंक्शन के मूल्य के बीच एक संबंध की खोज की, जो टेलर / एक्स (1 एक्स - 1) के टेलर श्रृंखला विस्तार में गुणांक हैं । (घातीय कार्य भी देखें।) अभी भी अधिक आश्चर्यजनक है, 1737 में यूलर ने ज़ेटा फ़ंक्शन से संबंधित एक सूत्र की खोज की, जिसमें सकारात्मक पूर्णांक वाले शब्दों का अनंत क्रम समाहित है, और एक अनंत उत्पाद जिसमें प्रत्येक अभाज्य संख्या शामिल है:
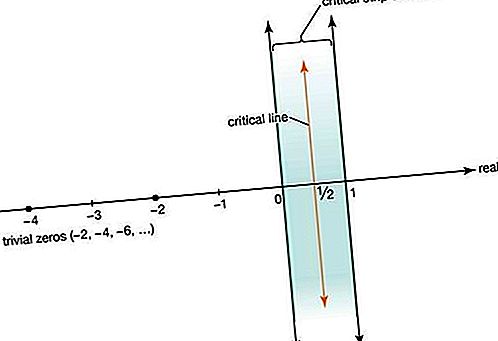
रीमैन ने जेट संख्या के अध्ययन को जटिल संख्या x + iy में शामिल करने के लिए विस्तारित किया, जहां i = वर्गमूल रूट √ the 1, जटिल विमान में लाइन x = 1 को छोड़कर। रीमैन को पता था कि ज़ेटा फ़ंक्शन सभी नकारात्मक के लिए शून्य के बराबर होता है यहां तक कि पूर्णांक −2, −4, the6,
।
(तथाकथित तुच्छ शून्य) और यह जटिल संख्याओं की महत्वपूर्ण पट्टी में अनंत संख्या में शून्य है, जो कि लाइनों x = 0 और x = 1. के बीच सख्ती से गिरता है। वह यह भी जानता था कि सभी nontrivial शून्य सम्मान के साथ सममित हैं महत्वपूर्ण लाइन एक्स = 1 / 2 । रीमैन ने अनुमान लगाया कि सभी nontrivial शून्य महत्वपूर्ण रेखा पर हैं, एक अनुमान है कि बाद में Riemann परिकल्पना के रूप में जाना जाता है।
1914 में अंग्रेजी गणितज्ञ गॉडफ्रे हेरॉल्ड हार्डी साबित कर दिया (रों) ζ के समाधान की एक अनंत संख्या = कि महत्वपूर्ण लाइन एक्स = पर 0 अस्तित्व 1 / 2 । इसके बाद विभिन्न गणितज्ञों द्वारा यह दिखाया गया कि समाधानों का एक बड़ा हिस्सा महत्वपूर्ण रेखा पर पड़ा होना चाहिए, हालांकि बार-बार "सबूत" कि सभी nontrivial समाधान उस पर दोषपूर्ण हैं। कंप्यूटर्स का उपयोग समाधानों के परीक्षण के लिए भी किया गया है, पहले 10 ट्रिलियन नॉटिवरियल समाधानों को महत्वपूर्ण रेखा पर झूठ दिखाया गया है।
रीमैन की परिकल्पना का एक प्रमाण संख्या सिद्धांत के लिए और क्रिप्टोग्राफी में primes के उपयोग के लिए दूरगामी परिणाम होगा।
रीमान की परिकल्पना लंबे समय से गणित में सबसे बड़ी अनसुलझी समस्या मानी जाती रही है। यह 10 अगस्त को गणितीय समस्याओं में से एक था (मुद्रित पते में 23) 20 वीं सदी के गणितज्ञों के लिए जर्मन गणितज्ञ डेविड हिल्बर्ट द्वारा पेरिस में दूसरी अंतर्राष्ट्रीय कांग्रेस गणित में 8 अगस्त, 1900 को एक चुनौती के रूप में प्रस्तुत किया गया था। 2000 में गणितज्ञ स्टीफन स्मेल ने हिल्बर्ट के विचार को 21 वीं सदी के लिए महत्वपूर्ण समस्याओं की एक सूची के साथ अद्यतन किया; रीमैन परिकल्पना नंबर एक थी। 2000 में इसे मिलेनियम प्रॉब्लम नामित किया गया, क्ले मैथमेटिक्स इंस्टीट्यूट ऑफ कैम्ब्रिज, मास।, यूएस द्वारा चयनित सात गणितीय समस्याओं में से एक को विशेष पुरस्कार के लिए। प्रत्येक मिलेनियम समस्या का समाधान $ 1 मिलियन है। 2008 में यूएस डिफेंस एडवांस्ड रिसर्च प्रोजेक्ट्स एजेंसी (DARPA) ने इसे DARPA गणितीय चुनौतियों, 23 गणितीय समस्याओं में से एक के रूप में सूचीबद्ध किया था, जिसके लिए यह फंडिंग के लिए अनुसंधान प्रस्तावों की मांग कर रहा था- “गणितीय चुनौती उन्नीस: सेटलान द रिहाना परिकल्पना। संख्या सिद्धांत के पवित्र कंघी बनानेवाले की रेती।